主线及互通匝道复曲线中间缓和曲线坐标计算

(本方法来自网上，未经验证)

1.复曲线中间缓和曲线

    复曲线是由两个或两个以上不同半径的同向圆曲线直接连接而成的曲线, 当两不同半径之比(R1/R2) 超出规定值(1.5—2) 时, 中间应插入一段缓和曲线, 这段缓和曲线并非是一条完整的缓和曲线, 而在插入时去掉了靠近半径无穷大方向的一段, 这种复曲线在高速公路主线、互通匝道应用较多, 关于中间缓和曲线坐标计算问题, 从测量资料上查不到具体计算方法。通过反复推敲验算比对高速公路主线、互通匝道复曲线中间缓和曲线设计坐标, 总结出复曲线中间缓和曲线坐标计算法。

    复曲线中间缓和曲线共有4 种类型计算分析:

    第一, 右转角大半径R 圆曲线与小半径r 圆曲线中间插入一段缓和曲线连接时, 先算出小半径r 缓和曲线ZH 点坐标、方位角及桩号,然后算出切线支距( x, y) , 通过ZH 点至YH 点之间坐标变换公式, 求出中间缓和曲线上任意桩号坐标。( 备注: y代负值)

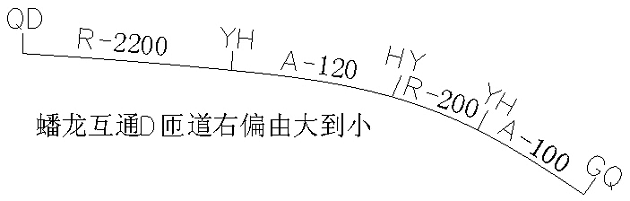
    第二, 右转角小半径r 圆曲线与大半径R 圆曲线中间插入一段缓和曲线连接时, 先算出小半径r 缓和曲线HZ 点坐标、方位角及桩号,然后算出切线支距( x, y) , 通过YH 点至HZ 点之间坐标变换公式, 求出中间缓和曲线上任意桩号坐标。( 注: y代负值)

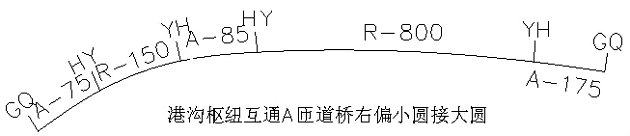
    第三, 左转角大半径R 圆曲线与小半径r 圆曲线中间插入一段缓和曲线连接时, 先算出小半径r 缓和曲线ZH 点坐标、方位角及桩号,然后算出切线支距( x, y) , 通过ZH 点至YH 点之间坐标变换公式, 求出中间缓和曲线上任意桩号坐标。( 注: y代负值)

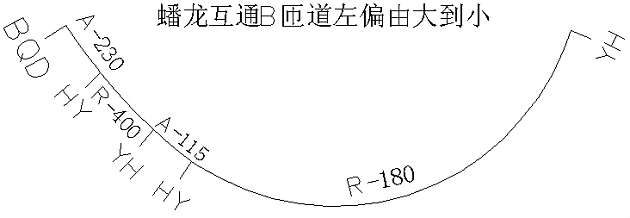
    第四, 左转角小半径r 圆曲线与大半径R 圆曲线中间插入一段缓和曲线连接时, 先算出小半径r 缓和曲线HZ 点坐标、方位角及桩号,然后算出切线支距( x, y) , 通过YH 点至HZ 点之间坐标变换公式, 求出中间缓和曲线上任意桩号坐标。( 注: y代正值)

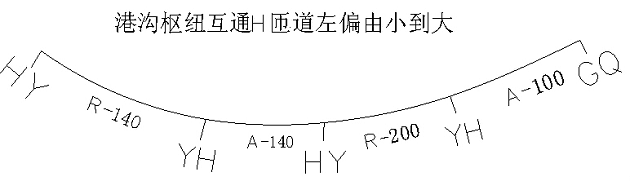
2.复曲线中间缓和曲线坐标计算步骤

    以右转角大半径R 圆曲线与小半径r 圆曲线中间插入一段缓和曲线连接类型为例:

    第一步: 根据中间缓和曲线参数, 求出大半径和小半径中间缓和曲线长度, 小半径与大半径中间缓和曲线长度之差, 就是中间缓和曲线长度;

    第二步: 根据小半径中间缓和曲线长度, 求出小半径中间缓和曲线角β0、1/3β0、2/3β0、弦长C 及弦线方位角θCX;

    第三步: 根据小半径缓和曲线HY 点坐标(XHY, YHY) 、桩号及第二步计算结果, 利用直线坐标计算公式, 求出小半径缓和曲线ZH 点坐标(XZH, YZH) 、方位角θZH 及桩号;

    第四步: 根据第三步计算结果, 利用缓和曲线参数方程, 求出中间缓和曲线上任意桩号切线支距, 然后利用坐标变换公式, 即可算出复曲线中间缓和曲线上任意桩号坐标。

3.计算实例

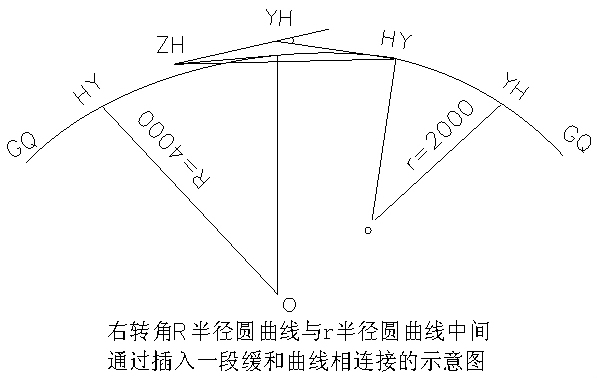
    以主线左幅GQ→HY→YH→HY→YH→GQ 一段右偏复曲线为例: 见下图

下表列出各主点设计桩号、半径、方位角、缓和曲线参数

    计算步骤详述如下:

    第一步: 求中间缓和曲线长度:

    ①大半径R 圆曲线两端缓和曲线长度:

    a.第一缓和曲线长: Ls1=A12/R=894.4272 /4000=200m

    b.第二缓和曲线长: Ls2=A22/R=774.5972 /4000=150m

    ②小半径r 圆曲线两端缓和曲线长度:

    a.第一缓和曲线长: S1=a12/r=774.5972/2000=300m

    b.第二缓和曲线长: S2=a22/r=632.4562/2000=200m

    ③小半径圆曲线第一缓和曲线半径由r=2000m 渐变到无穷大的过程中, 必有一点其半径等于4000m, 与大半径圆曲线YH 点相接, 于是R 半径圆曲线与r 半径圆曲线中间就出现一段缓和曲线, 其长度: L中=S1- LS2=300- 150=150m, 或用以下公式计算L 中=A2 (R- r) /Rr=

774.5972(4000- 2000)/4000×2000=150m

    第二步: 求r 半径中间缓和曲线角β0、1/3β0、2/3β0、弦长C 及弦线方位角θCX;

    ①计算r 半径圆曲线第一缓和曲线角:

    β0=90S1/πr=90×300/2000π=4°17'49.86"

    1/3β0=1°25'56.62"    2/3β0=2°51'53.24"

    ②计算r 半径缓和曲线弦长C 及弦线方位角θcx:

    C=S1- S13/90r2=300- 3003/90×20002=299.925

    θCX =θHY - 2β0/3 +180°=89°01'36.12" - 2°51'53.24" +180°=266o09'42.88"

    第三步: 计算r 半径缓和曲线ZH 点坐标、方位角及桩号( 实际不存在, 只作辅助计算用)

    已知r 半径HY 点:

    (1) 坐标: XHY=4055027.224, YHY=474097.784

    (2) 方位角θHY=89°01'36.12"

    (3)HY 点桩号LK5+048.693

    求出ZH 点坐标(XZH, YZH) 、方位角θZH 及桩号

    ①ZH 点坐标(XZH, YZH)

    XZH =XHY +CcosθCX =4055027.224 +299.925cos266°09'42.88" =4055007.148

    YZH =YHY +CsinθCX =474097.784 +299.925sin266°09'42.88" =473798.532

    ②方位角:θZH=θHY-βo=89°01'36.12″- 4°17'49.86″=84°43'46.26″

或θZH=θCX-βo/3=86°09'42.88"- 1°25'56.26"=84°43'46.26"

    ③ZH 点桩号等于r 半径HY 点桩号减第一缓和曲S1

    即LK5+048.693- 300=LK4+748.693

    第四步: ①.计算中间缓和曲线上任意点切线支距:

    以r 半径缓和曲线起点ZH 点为坐标原点, 以切线为X 轴, 过ZH点且垂直于切线的垂线为Y 轴, 利用缓和曲线参数方程:

    X=L?L5/(40r2s12)+L9/3456r4s14(注: 半径大时可略去高次项)

    y=L3/6rs1- L7/336r3s13 计算出所求桩号切线支距。

    ②利用坐标变换公式: 计算中间缓和曲线中桩坐标

    X=XZH+xcosθZH- ysinθZH

    Y=YZH+xsinθZH+ycosθZH(注意: 曲线右转角Y 代正值, 曲线左转角Y代负值)

以下表所列4 个桩号为例: 计算中间缓和曲线中桩切线支距和坐标

切线支距、中桩坐标计算表

4.结束语

    上述计算法只要掌握切线支距法, 利用坐标变换公式就能准确快速的计算出复曲线中间缓和曲线上任意桩号坐标。